仕事算の解き方を簡単にする2つの量 中学受験プロ講師ブログ
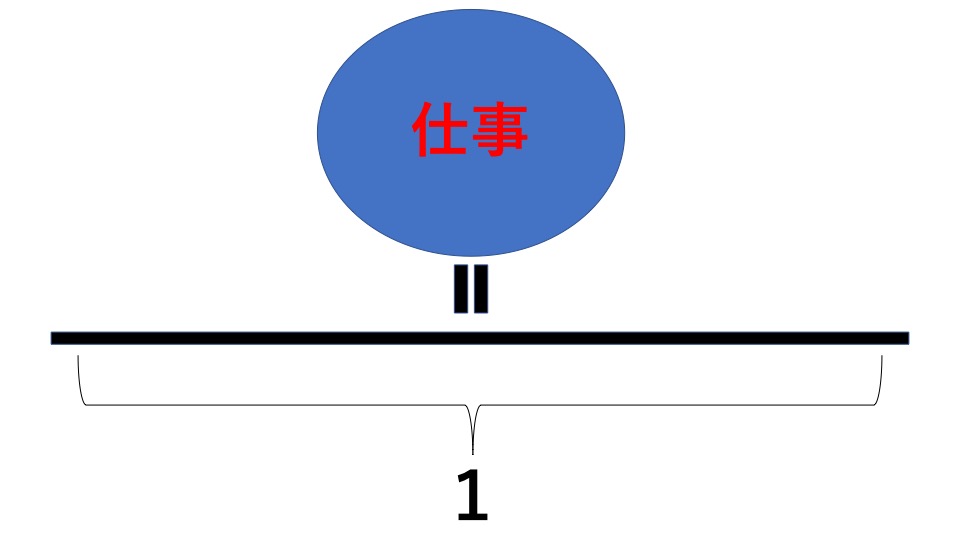
仕事算の解き方 全仕事量を1または最小公倍数として考える。 単位時間あたりにする仕事量 ・1人で仕事をする場合: この仕事をAとBの2人で いっしょにやると何分かかるか? mazuha kanarazu jibunde kangaetene! 解答解説 「仕事全体の量」を、160と240の最小公倍数「480」とする。 まず、AB各々の「仕事能率」を求めます。 A1人で1分あたり 480÷160=3(Aの仕事能率) B1人で1分
仕事算 解き方 最小公倍数
仕事算 解き方 最小公倍数- 最小公倍数 です。 今日解く問題では、この2つの求め方を使って計算する必要があります。 がんばって解いて行きましょう〜! 「 数の性質 」の問題に 挑戦 ちょうせん ! ある整数xと84の最大公約数は21で、最小公倍数は252です。整数xを求めなさい。「倍数算」の解き方とポイント|3つのパターンを数直線で解説 管理人 11月 15, 18 / 7月 10, 21 数量関係をしっかり抑えた上で数直線などを使いこなして解く問題です。
仕事算の解き方 基礎から応用まで問題を使ってイチから解説するぞ 数スタ
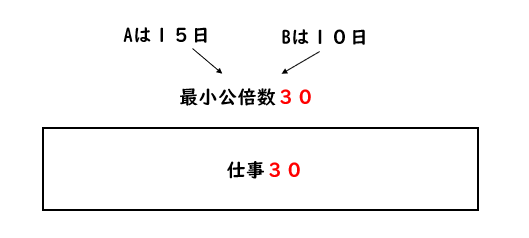
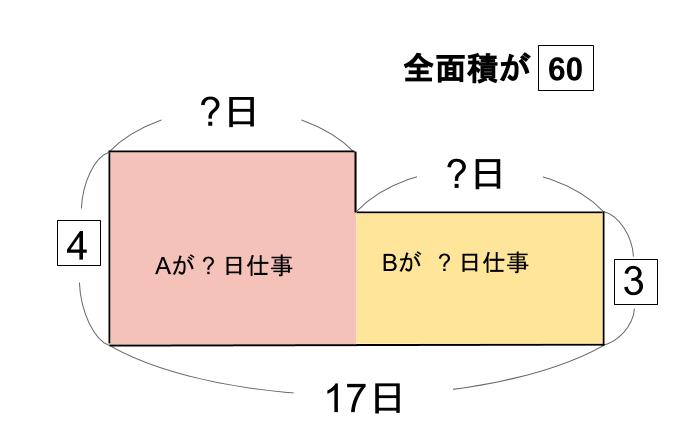
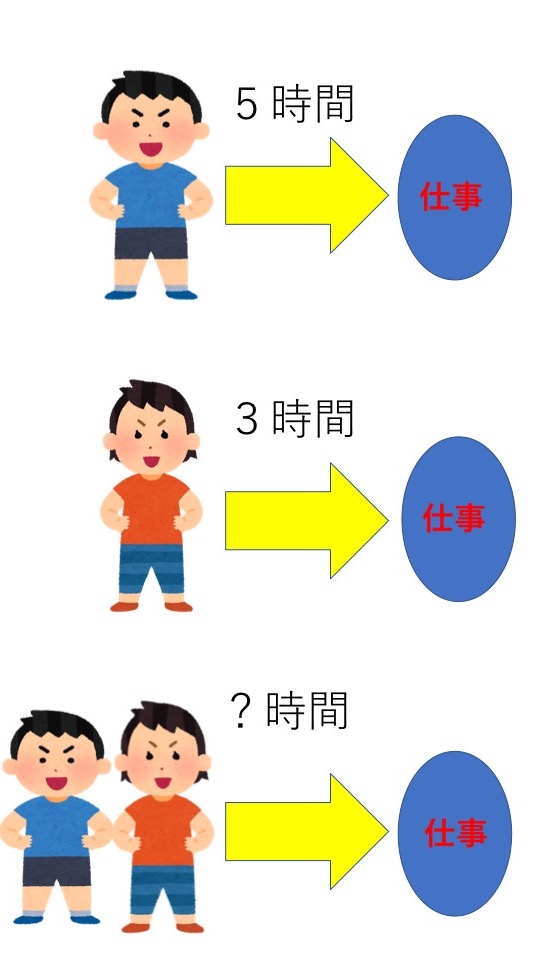
SPI 仕事算・水槽算 <注意!> この動画の指導法は、数学が苦手な方に向けた指導法です。問題集等にある解き方とは異なります。 仕事算・例題(1)<問題> ある仕事をするのに、Pさん1人では8日間かかり、Qさん1人では1 なぜ最小公倍数に設定するといいのか。 やってみれば分かります。 60 ÷ 日 = 3A君が1日でやる仕事 60 ÷ 30日 = 2B君が1日でやる仕事 3 + 2 = 5・・・A君B君が1日でやる仕事 60 ÷ 5 = 12日 どうですか? 全体を最小公倍数の60に設定すると、 ぜ~んぶ整数で計算できますね。 カンタン! 全体量はいくつに設定してもOK! 答えは変わりません。 "何をいくつに設定する 最大公約数と最小公倍数の計算プリント 3の倍数の性質と見分け方(3の倍数早見表つき) 中学受験によく出る部分分数分解の問題と解き方 小学校で習う面積の公式まとめ 多角形の対角線の本数(公式と証明) つるかめ算の面積図による解き方と
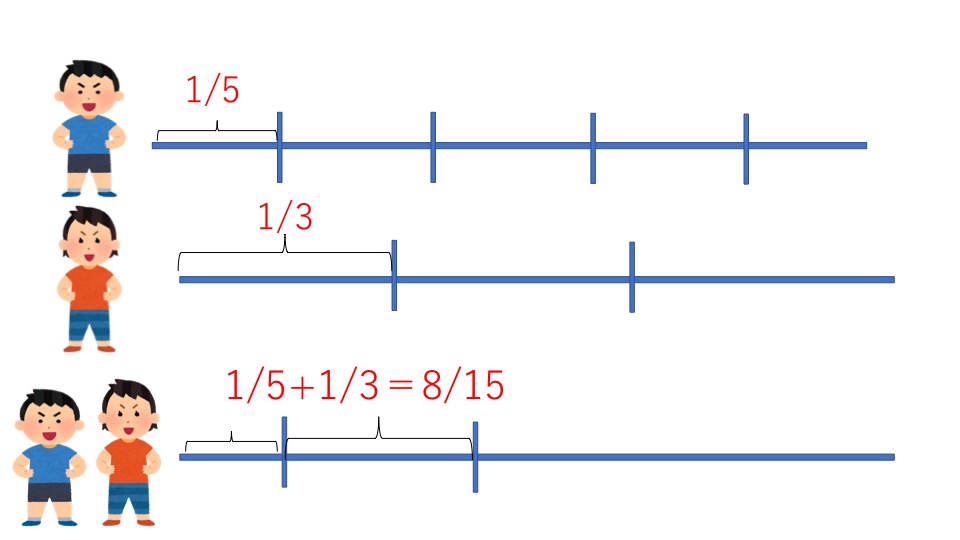
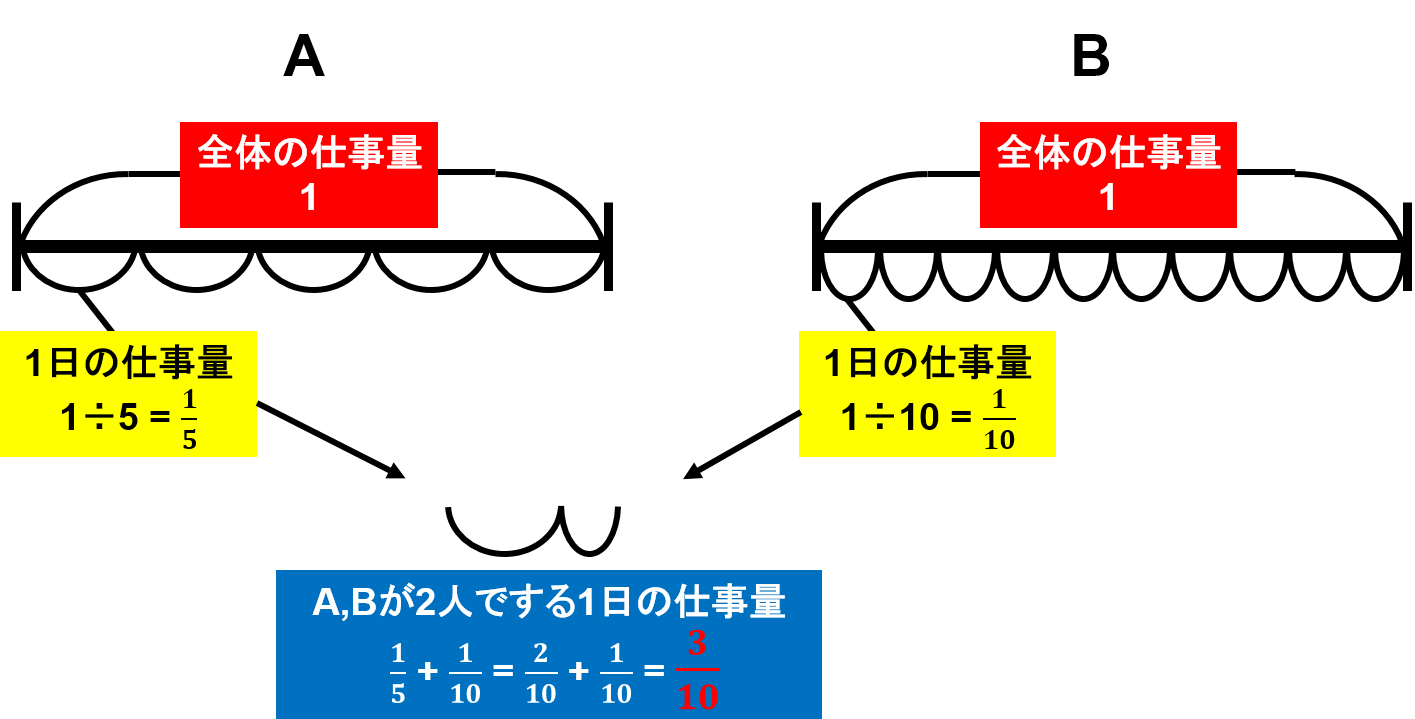
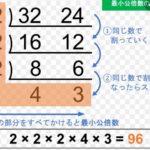
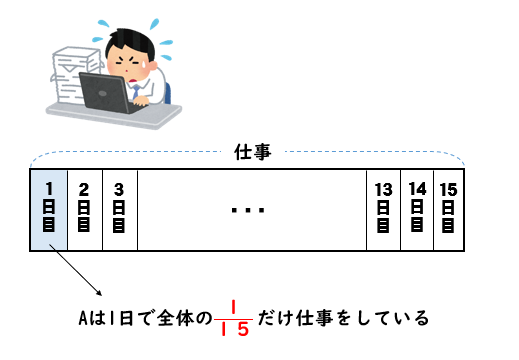
このように、この問題を「仕事全体を1」で解くには、チョッとした技術が必要なんです。 では、「最小公倍数解法」ではどうなるのでしょうか? 仕事算の最小公倍数解法は、「仕事全体=仕事をする日数の最小公倍数」が基本ですね。 すると 仕事算は最小公倍数の問題です。 解き方は色々ありますので、お子さんのお好きな解き方で。 例えば Aさんの一日の仕事量は1/18 bさんの一日の仕事量は1/15 と表現する場合の答えを求める式は となります。 最小公倍数とは、 つ以上の自然数の公倍数(= 共通の倍数)の中で最小のもの です。 例えば、 と の最小公倍数を考えてみましょう。 の倍数 , , , , , の倍数 , , , , , , , と の公倍数(共通の倍数)は です。 これらのうち最小のもの(最小公倍数)は となります。 最小公倍数の求め方 それぞれの倍数を並べていけばいずれ最小公倍数が見つかりますが、毎回しらみつぶしに調べるのは
仕事算 解き方 最小公倍数のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  |  |
 |  | |
「仕事算 解き方 最小公倍数」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 | 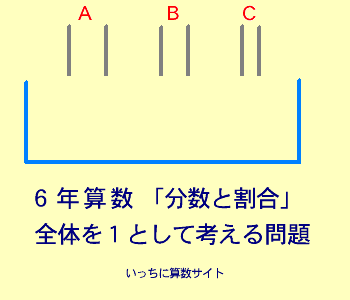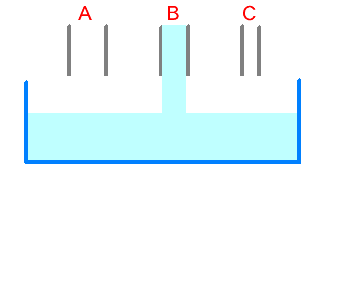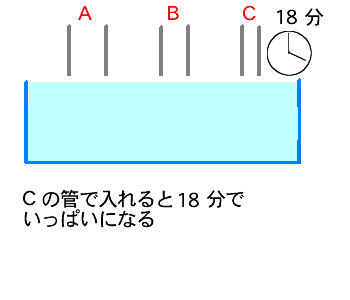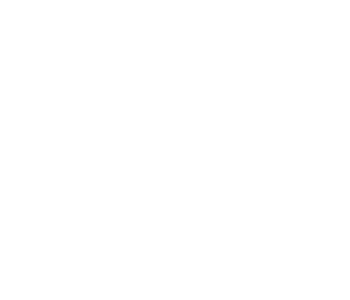 | |
「仕事算 解き方 最小公倍数」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「仕事算 解き方 最小公倍数」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 |  | |
「仕事算 解き方 最小公倍数」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
「仕事算 解き方 最小公倍数」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 | ||
「仕事算 解き方 最小公倍数」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「仕事算 解き方 最小公倍数」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「仕事算 解き方 最小公倍数」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 |  | |
「仕事算 解き方 最小公倍数」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 | ||
「仕事算 解き方 最小公倍数」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「仕事算 解き方 最小公倍数」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
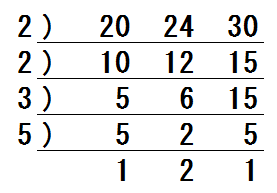
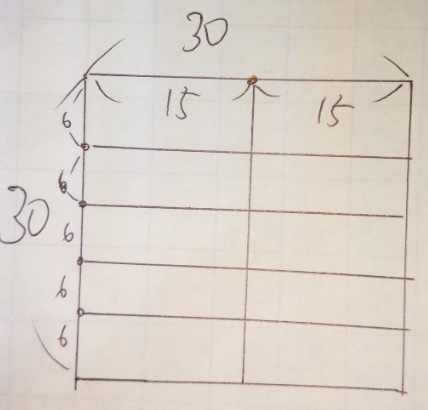
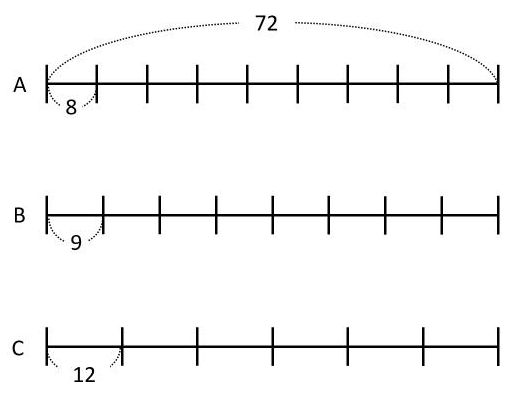
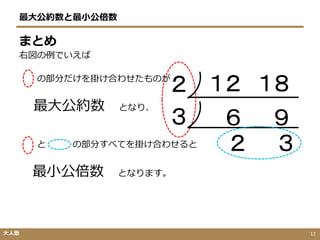
最大公約数、最小公倍数の求め方の代表は連除法(はしご算)ですね。 R=9 Qは72の約数で9と互いに素なので、 Q=1、2、4、8 の 4通り が考えられます。 この本の解き方 仕事量全体を10と6の最小公倍数である30とする。 甲の1日あたりの仕事量は、30÷10=3 である。 甲と乙の1日あたりの仕事量は、30÷6=5 である。 よって、乙の1日あたりの仕事量は、53=2 と分かった。
Incoming Term: 仕事算 解き方 最小公倍数,




0 件のコメント:
コメントを投稿